
Introduction:
In the evolving landscape of digital finance, game theory significantly influences the structure and function of decentralized networks. This exploration sheds light on the intricate relationship between game theory and cryptocurrencies, highlighting how strategic interaction models impact blockchain operations. We'll examine the influence of key game theory concepts like Nash Equilibrium and the Prisoner's Dilemma on the behaviors of network participants, including miners and users, providing a comprehensive insight into the crypto ecosystem for enthusiasts, trading algorithm users and scholars alike.
Understanding Game Theory
Game theory is a branch of mathematics that studies strategic interactions, meaning situations where the outcome for each participant or 'player' depends on the actions of all. In the context of cryptocurrencies, the players can be miners, users, or even the cryptocurrency networks themselves.
A fundamental concept in game theory is the Nash Equilibrium, named after the mathematician John Nash. In a Nash Equilibrium, each player chooses their best strategy, given the strategies chosen by the other players, and no player can benefit from changing their strategy while the other players keep theirs unchanged.
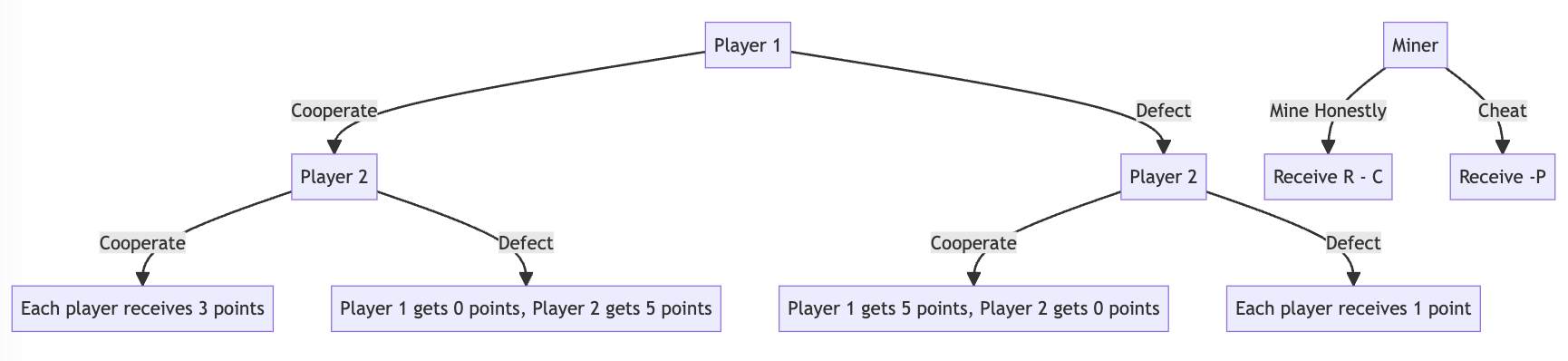
To illustrate this, let's consider a simplified game with two players. Each player can choose either to cooperate (C) or to defect (D). The payoffs for each combination of strategies are as follows:
- (C, C): Each player receives 3 points.
- (D, D): Each player receives 1 point.
- (C, D) or (D, C): The player who defects gets 5 points, and the one who cooperates gets 0.
In this game, the Nash Equilibrium is (D, D), even though both players would be better off if they could trust each other to cooperate. This is because, no matter what the other player does, each player can always get a higher payoff by defecting. This situation is known as the Prisoner's Dilemma.
Game Theory and Cryptocurrencies
In the cryptocurrency space, game theory comes into play in various ways. One of the most significant is in the process of mining, where participants in the network compete to add the next block to the blockchain.
Miners must solve complex mathematical problems, and the first one to find the solution gets to add the new block and receive a reward in cryptocurrency. This process is known as Proof of Work. The difficulty of the problems ensures that it's costly to participate in the mining process, which discourages dishonest behavior.
Let's consider a scenario where a miner has the option to mine honestly or attempt to cheat the system by creating an invalid block. If they mine honestly, they incur a cost (C) for the computational resources used and receive a reward (R) if they successfully add a block. If they cheat, they still incur the cost, but they also run a risk (P) of being detected and penalized.
The payoff matrix for this game could look something like this:
- (Honest, Honest): Each miner receives R - C.
- (Cheat, Cheat): Each miner receives -P.
- (Honest, Cheat) or (Cheat, Honest): The honest miner receives R - C, and the cheating miner receives -P.
In this game, the Nash Equilibrium is (Honest, Honest), assuming that the reward for mining a block is greater than the cost, and the penalty for cheating is severe enough. This equilibrium helps maintain the integrity of the cryptocurrency network.
Conclusion: The Interplay of Game Theory and Cryptocurrencies
Game theory's strategic models are instrumental in sustaining the equilibrium within the decentralized architecture of cryptocurrencies. This analytical framework not only underpins the crypto world but also has broader applications in digital and peer-to-peer networks. The synergy between game theory and cryptocurrencies is pivotal, steering innovation and bolstering trust in decentralized platforms.
This mathematical framework extends beyond cryptocurrencies, finding relevance in various digital systems and peer-to-peer networks. As we delve deeper into the realm of digital currencies and blockchain technology, game theory's insights remain invaluable, guiding us towards more secure and efficient decentralized systems.
In essence, the relationship between game theory and cryptocurrencies is not merely an academic exploration but a critical component shaping the future of digital currencies. This interplay will continue to drive innovation and foster trust in these decentralized systems.

Happy Trading,
Website: https://kryll.io
Twitter: @Kryll_io
Telegram EN: https://t.me/kryll_io
Telegram FR: https://t.me/kryll_fr
Telegram ES: https://t.me/kryll_es
Discord: https://discord.gg/PDcHd8K
Reddit: https://reddit.com/r/Kryll_io
Facebook: https://www.facebook.com/kryll.io
Support: support@kryll.io


