Comprendre les crypto-monnaies sous le prisme de la théorie des jeux

Introduction :

Dans le monde des crypto-monnaies, les principes de théorie des jeux jouent un rôle essentiel dans le maintien de l'intégrité et de la fonctionnalité des systèmes décentralisés. Cet article se penche sur le fascinant croisement de la théorie des jeux et des crypto-monnaies, en élucidant la manière dont les modèles de prise de décision stratégique influencent les opérations dans la blockchain. Des actions des mineurs au comportement des utilisateurs, nous explorerons comment les principes de la théorie des jeux, tels que l'équilibre de Nash et le "Dilemme du prisonnier", façonnent le paysage des crypto-monnaies. Que vous soyez un passionné crypto-monnaie et/ou blockchain, un spécialiste de la théorie des jeux, un lecteur curieux, un trader ou un utilisateur de bots de trading, ce guide complet vous permettra de mieux comprendre les mécanismes complexes qui régissent le monde des cryptos.

Comprendre le phénomène de théorie des jeux

La théorie des jeux est une branche des mathématiques qui étudie les interactions à caractère stratégique, c'est-à-dire les situations dans lesquelles le résultat pour chaque participant ou "joueur" dépend des actions de tous. Dans le contexte des crypto-monnaies, les joueurs peuvent être des mineurs, des utilisateurs ou même les réseaux de crypto-monnaies (blockchain) eux-mêmes.

L'équilibre de Nash, du nom du mathématicien John Nash, est un concept fondamental de la théorie des jeux. Dans un équilibre de Nash, chaque joueur choisit sa meilleure stratégie en fonction des stratégies choisies par les autres joueurs, et aucun joueur ne peut tirer profit d'un changement de stratégie puisque que les autres joueurs ne modifient pas la leur.

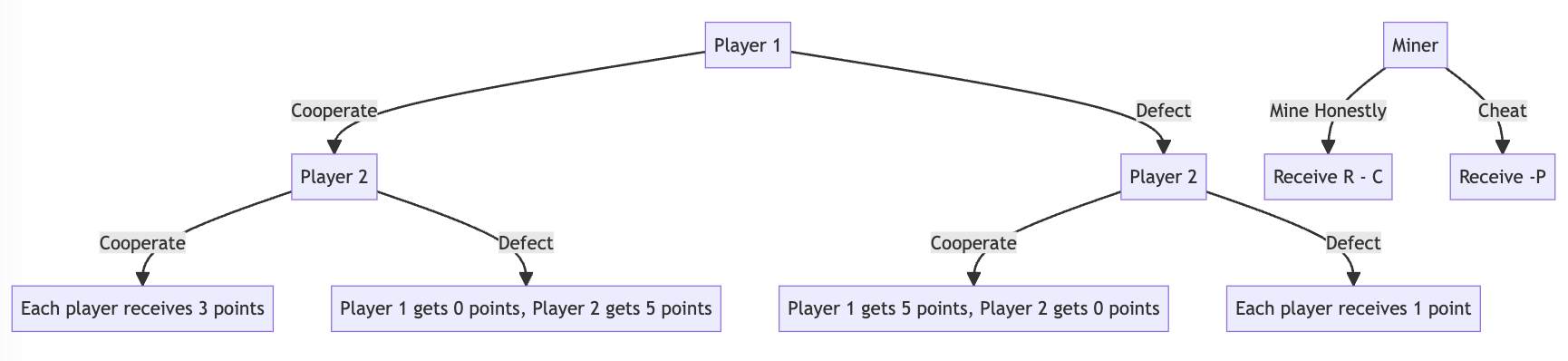
Pour illustrer cela, imaginons un jeu simple composé de deux joueurs. Chaque joueur peut choisir de coopérer (C) ou de rivaliser (D). Les gains pour chaque combinaison de stratégies sont les suivants :

(C, C) : Chaque joueur
(D, D) : Chaque joueur reçoit 1 point.
(C, D) ou (D, C) : Le joueur qui fait défaut reçoit 5 points, et celui qui coopère en reçoit 0.

Dans ce jeu, l'équilibre de Nash est (D, D), même si les deux joueurs seraient plus avantagés s'ils pouvaient se faire confiance pour coopérer. En effet, quoi que fasse l'autre joueur, chaque joueur peut toujours obtenir un gain plus élevé en choisissant de rivaliser avec l'autre joueur. Cette situation est connue sous le nom de "Dilemme du prisonnier".

Théorie des jeux et crypto-monnaies

Dans le monde des crypto-monnaies, la théorie des jeux entre en jeu de diverses manières. L'une des plus importantes est le processus de minage, où les participants au réseau rivalisent pour ajouter le prochain bloc à la blockchain.

Les mineurs doivent résoudre des problèmes mathématiques complexes, et le premier à trouver la solution ajoute le nouveau bloc et reçoit une récompense. Ce processus est connu sous le nom de "Preuve de travail" (Proof of Work ou PoW). La difficulté des problèmes fait qu'il est coûteux de participer au processus de minage, ce qui décourage les comportements malhonnêtes.

Prenons par exemple un scénario dans lequel un mineur a la possibilité de miner honnêtement ou de tenter de tromper le système en créant un bloc invalide. S'il mine honnêtement, il encourt un coût (C) pour les ressources informatiques utilisées et reçoit une récompense (R) s'il réussit à ajouter un bloc. S'il triche, il supporte toujours le coût, mais il court également le risque (P) d'être remarqué et pénalisé.

La matrice des gains pour ce jeu peut se présenter comme suit :

(Triche, Triche) : Chaque mineur reçoit -P.
(Honnêteté, Triche) ou (Triche, Honnêteté) : Le mineur honnête reçoit R - C, et le mineur malhonnête reçoit -P.

Dans ce jeu, l'équilibre de Nash est (Honnête, Honnête), en supposant que la récompense pour l'extraction d'un bloc est supérieure au coût et que la pénalité pour tricherie est suffisamment lourde. Cet équilibre permet de maintenir l'intégrité d'une blockchain.

Conclusion : Relations entre la théorie des jeux et les crypto-monnaies

La théorie des jeux, avec ses modèles de prise de décision stratégique tels que l'équilibre de Nash et le "Dilemme du prisonnier", sert de cadre dans le monde complexe des crypto-monnaies. Elle permet de maintenir l'équilibre de ces systèmes décentralisés, en veillant à ce que chaque participant contribue à la stabilité et à la sécurité de l'ensemble du réseau.

Ce cadre mathématique s'étend au-delà des crypto-monnaies et trouve sa pertinence dans divers systèmes numériques et réseaux pair-à-pair. Alors que nous approfondissons le domaine des monnaies numériques et de la technologie blockchain, les perspectives de la théorie des jeux restent inestimables, nous guidant vers des systèmes décentralisés plus sécurisés et plus efficients.

Par essence, la relation entre la théorie des jeux et les crypto-monnaies n'est pas une simple étude scientifique, mais un élément essentiel qui façonne l'avenir des monnaies numériques. Cette relation continuera à favoriser l'innovation et à renforcer la confiance dans ces systèmes décentralisés.